Самое актуальное и обсуждаемое
Популярное
Полезные советы
Важно знать!
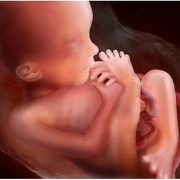
22 неделя беременности (2 триместр)Особые рекомендации Для избегания растяжек можно попробовать купаться под контрастным душем. Чередуйте не сильно холодную и теплую воду. Это не только придаст эластичности вашей коже, но и закалит вас...
Читать далее 12 природных средств от простуды и гриппа 10 симптомов туннельного синдрома кисти: что это такое и как лечить? 12 неделя беременности 10 этапов лечения пародонтоза 40 советов как быстро не кончать мужчине, что делать, куда «бежать» 41 неделя беременности, когда начнутся роды? признаки скорых родов 4 метода лечения кандидозного моллюска 10 частых причин, из-за которых может болеть зуб 29 неделя беременности
Рекомендуем
Лучшее

Важно знать!
17 продуктов, которые вредны при заболеваниях почекДиета № 7 в по Певзнеру Суть диетического стола №7в состоит в строгом ограничении экстрактивных веществ, содержащихся в мясе и грибах, уменьшении белка в меню.
Показания:
Нефротический синдром при хронических...
Читать далее 31-я акушерская неделя: что происходит в организме, возможные проблемы 10 правил женской гигиены, о которых вы должны знать 19 неделя беременности 6 самых распространенных заболеваний легких 37, 38, 39 недели беременности: предвестники родов у повторнородящих 4d узи при беременности 10 простых способов узнать, каков человек на самом деле 15 признаков, что у вас дефицит железа в организме 24 богатых протеином продукта для больших мышц
Новое
Обсуждаемое

Важно знать!
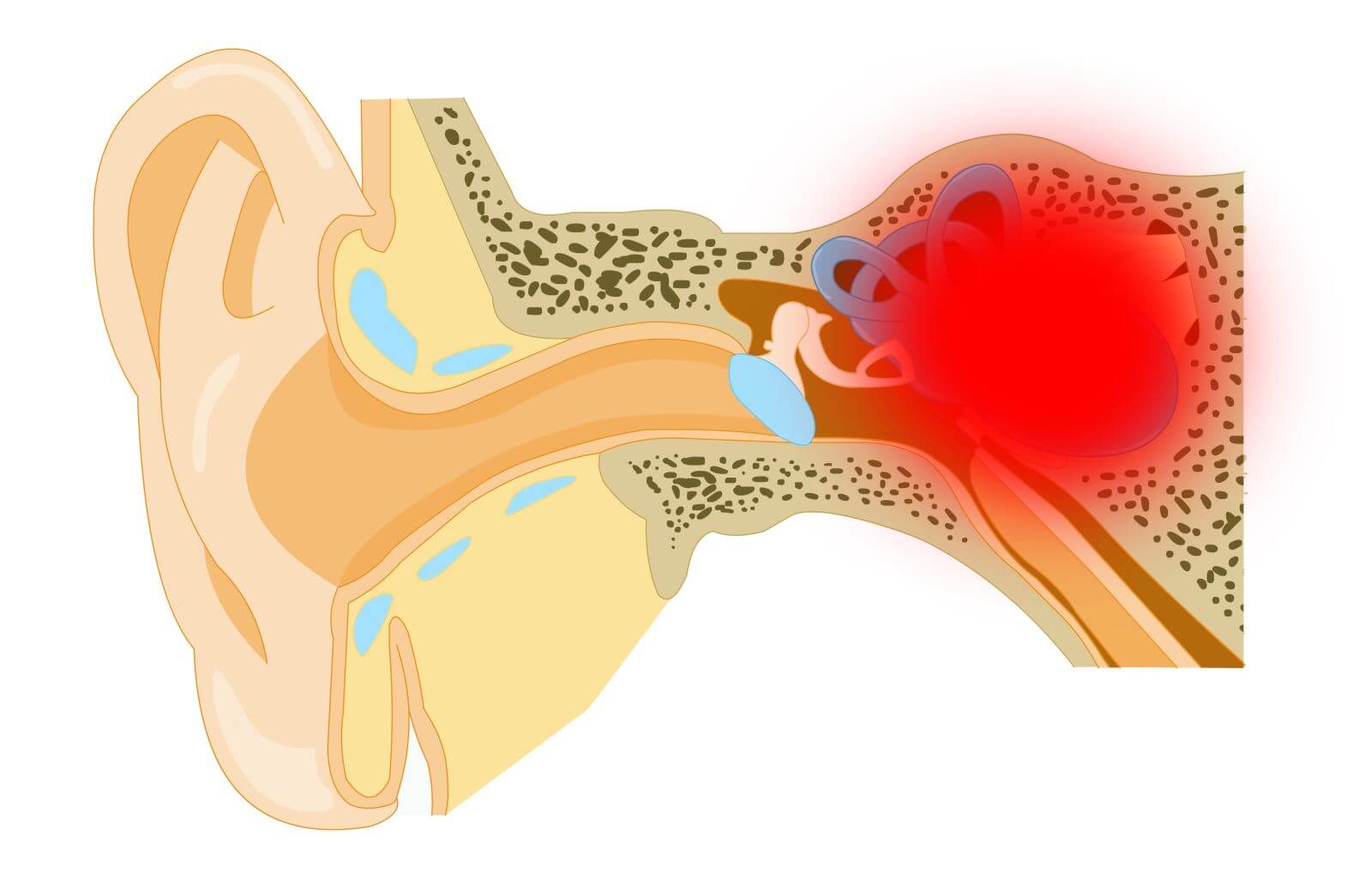
5 признаков того, что вам не хватает кислородаКислородное голодание у плода и новорожденного Кислородное голодание оказывает весьма неблагоприятное действие на развивающийся при беременности плод, клетки которого постоянно размножаются, формируя...
Читать далее 13 аптечных кремов для лица 20 действенных методов очистки печени и кишечника 10 лучших средств от герпеса 10 распространенных причин боли внизу живота справа 15 типов масок. какая от чего защищает 9 неделя беременности 1 неделя беременности 3 способа вылечить генитальный герпес у женщин, как он выглядит, можно ли заниматься сексом 7 лучших мазей с антибиотиком для заживления раны
Популярное
Актуальное
Важно знать!
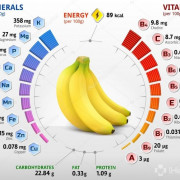
7 научно обоснованных причин есть бананы каждый деньПольза и вред банана для организма человека Популярность бананов обусловлена несомненными вкусовыми качествами, питательной ценностью и пользой для организма большинства обитателей земного шара. Давайте...
Читать далее 10 правил первой помощи при приступе эпилепсии, которые должны знать все 14 лучших слабительных средств 16 признаков душевного здоровья 14 целебных элемента иван-чая для женщин 9 лучших лекарств от сухого кашля 10 ранних симптомов шизофрении, которые нельзя пропустить 15 лучших отхаркивающих средств 10 признаков дефицита меди в организме, которые можно заметить и без анализов 5 основных причин по которым болит живот и тошнит
Обновления
 Статьи Почему долго не проходят синяки — секреты долговечности синяков?
Статьи Почему долго не проходят синяки — секреты долговечности синяков? Почему долго не проходят синяки? Синяки – это одна из самых распространенных травм, которые часто...
 Статьи Частота чистки лица у косметолога: советы для здоровой кожи.
Статьи Частота чистки лица у косметолога: советы для здоровой кожи. Секреты эффективной подготовки и ухода за кожей
Выбор процедур по уходу за кожей лица требует внимательного...
 Статьи Пансионат для престарелых и инвалидов: уютное проживание, качественный уход и медицинская забота.
Статьи Пансионат для престарелых и инвалидов: уютное проживание, качественный уход и медицинская забота. Пансионаты для престарелых людей становятся все более значимой частью нашего общества в условиях увеличивающегося...
 Лекарства Детский ортопед: когда обратиться и какие заболевания – руководство для родителей.
Лекарства Детский ортопед: когда обратиться и какие заболевания – руководство для родителей. Детский ортопед: заболевания и когда обратиться к специалисту
Детское здоровье является одним из самых...
 Особенности лечения в медицинских центрах
Особенности лечения в медицинских центрах Качество лечения «Мне поставили неправильный диагноз, при этом меня постоянно гоняли от одного врача...
 7 основных и множество дополнительных причин онемения рук и пальцев
7 основных и множество дополнительных причин онемения рук и пальцев Немеют пальцы правой руки, кисть ↑ Если онемение возникает не во всей руке, а только в пальцах, это...
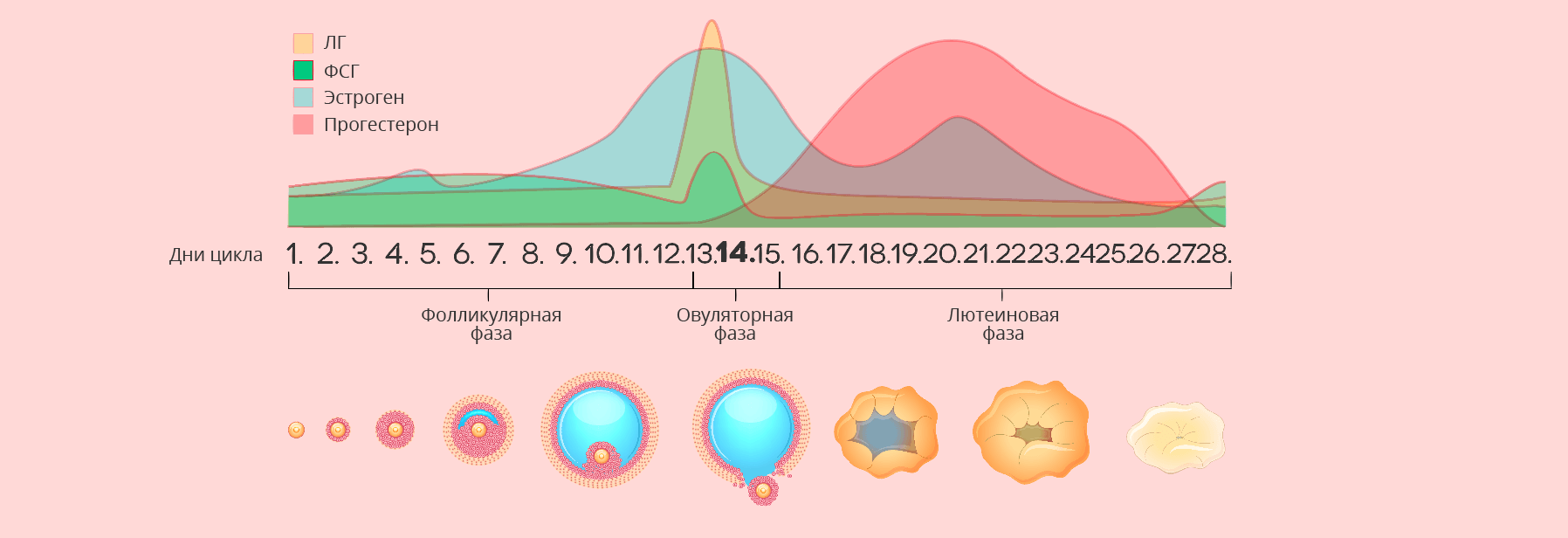 12 штрихов к портрету вагины: знания, которые спасут ваш секс
12 штрихов к портрету вагины: знания, которые спасут ваш секс Как возникает вагинальный оргазм? Второй тип женского оргазма — влагалищный. Эрогенным полем при этом...
 100 способов лечения хреном
100 способов лечения хреном Употребление для лечения различных заболеваний Сахарный диабет
Хрен при диабете не просто разрешен,...
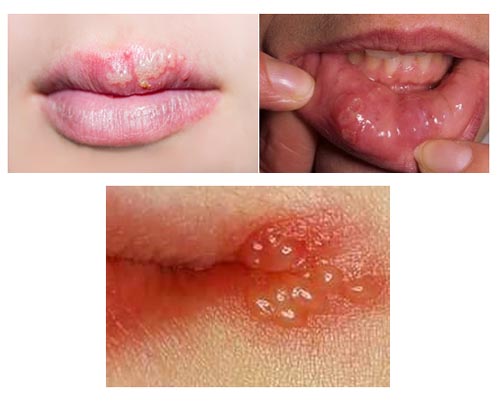 15 лучших средств от герпеса
15 лучших средств от герпеса Общие сведения Подавляющее большинство людей неоднократно сталкивалось с явлением «простуды на губах»,...
 Беременность 18 неделя беременности
Беременность 18 неделя беременности Замершая беременность Многие наслышаны о замершей беременности, о которой женщина длительное время может...
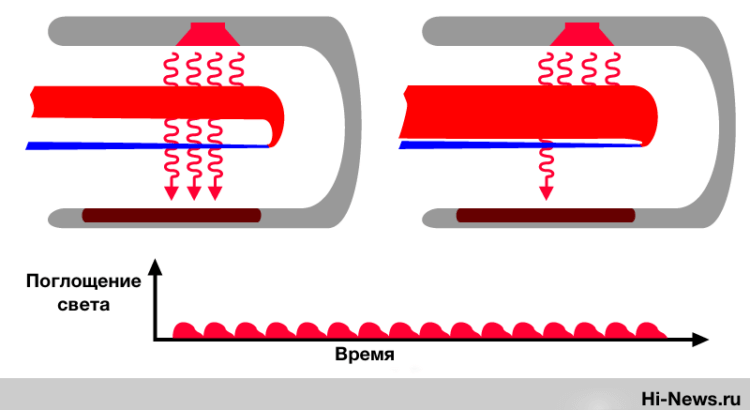 6 лучших оксиметров
6 лучших оксиметров Лучшие медицинские оксиметры Медицинский портативный оксиметр прост в использовании. Он позволяет делать...
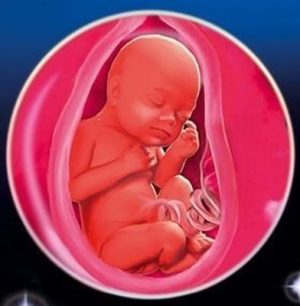 Беременность 27 неделя беременности: что происходит с женщиной и ребенком
Беременность 27 неделя беременности: что происходит с женщиной и ребенком Когда необходима консультация врача? Следует знать, при появлении каких симптомов нужно вызвать скорую...